DEFINICIÓN DE ECUACIÓN LINEAL
Una ecuación es una expresión algebraica en la cual se manifiesta una igualdad. Pueden tener una o más incógnitas.
En el caso de las ecuaciones de primer grado, son aquellas en que la incógnita en la ecuación tiene exponente uno, las de segundo grado tienen exponente dos, las de tercer grado exponente tres y así.
Las Ecuaciones Lineales son ecuaciones de primer grado las cuales se pueden representar en un sistema cartesiano (plano cartesiano o espacio cartesiano). Una forma de ecuación lineal es la Ecuación de la recta (o también se le conoce como ecuación con dos incógnitas). Otra forma de ecuaciones lineales es la Ecuación con una incógnita.
Ejemplo de ecuación de la recta: 5x = 10
Otro ejemplo de ecuación lineal: y = 2x – 1
¿Estás aprendiendo acerca de este tema y necesitas algunos ejemplos de ecuaciones lineales resueltas para practicar?
Has llegado al lugar indicado, porque hoy aquí te propongo ejercicios de ecuaciones lineales resueltas y además verificadas.
Has llegado al lugar indicado, porque hoy aquí te propongo ejercicios de ecuaciones lineales resueltas y además verificadas.
Están en orden, y el criterio elegido es que las primeras sean más sencillas y las siguientes más difíciles.
En este último caso, he elegido aportar algunas explicaciones al momento de resolverla y te muestro el “paso a paso” en una imagen , ya que ello permite que se vea con mayor claridad el trabajo con denominadores.
Te sugiero que intentes resolverlos autónoma mente y no te rindas fácilmente a consultar el proceso de solución. En el caso que lo hagas, vuelve a apartarte e intenta hacerlos por tí mismo. Es momento de timar lápiz y papel y comenzar a trabajar con estos…
Ejemplos de ecuaciones lineales resueltas
Ejercicio 1
- Soluciones
Detalle de los pasos de resolución y explicaciones:
 1) Primero se pretende “eliminar” el denominador 28 del segundo miembro; para ello se multiplican ambos miembros por 28, de modo que en el segundo miembro el producto se eliminará con el denominador. En el caso del primer miembro se podrán hacer las divisiones con los respectivos denominadores, de modo que 28/4 queda en un factor 7 y 28/7 queda en el factor 4.
1) Primero se pretende “eliminar” el denominador 28 del segundo miembro; para ello se multiplican ambos miembros por 28, de modo que en el segundo miembro el producto se eliminará con el denominador. En el caso del primer miembro se podrán hacer las divisiones con los respectivos denominadores, de modo que 28/4 queda en un factor 7 y 28/7 queda en el factor 4.2) Se realizan los productos distributivos que quedan planteados (habiendo eliminado ya los denominadores correspondientes)
3) Se agrupan los términos en x en el primer miembro de la igualdad y los términos sin x en el segundo miembro.
4) Se realizan operaciones y se halla el resultado final.
Ejercicio 2
Solución:
Como no existen signos de agrupación, omites el primer paso del procedimiento.
Recuerda que puedes comprobar el resultado obtenido, sustituyendo el valor hallado en la ecuación original.
Ejercicio 3
Solución:
Aplicando cada paso del procedimiento indicado obtienes:
Como la ecuación tiene denominador, una vía de solución puede ser eliminarlo multiplicando toda la ecuación por 3 o transpones el 3 al miembro izquierdo multiplicando al binomio.
R/ 
Nota:También puedes resolver esta ecuación sin necesidad de eliminar los denominadores, es decir, agrupas las variables en uno de los miembros y los términos independientes en el otro, reduces los términos semejantes y despejas la variable.
Algunos vídeos para que entiendan mejor....
3er vídeo:
4to vídeo:
OBJETIVO DEL BLOG
- Este blog fue creado con el fin de aprender más sobre este tema maravilloso, de una manera didáctica. Y de este modo llegar a ustedes a través de vídeos y podamos ver que las matemáticas no son tan complicadas como parecen. Espero que les guste este blog, que hicimos con mucho cariño para ustedes.
Bibliografía:
Libro:
*Matemáticas aplicadas a la Administración
y a la Economía.
Autores:
- *Jagdish C. Arya
- *Robin W. Lardner
Libro:
*Matemática: Razonamiento y Aplicaciones.
Autores:
Autores:
- *Charles D. Miller
- *Vern E. Heeren
- *John Hornsby

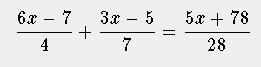
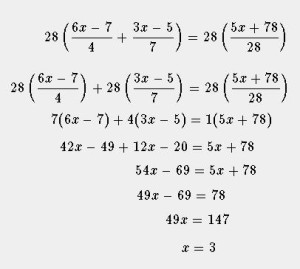






No hay comentarios.:
Publicar un comentario